Square the Square
This is the result of a challenge from Karl Scherer, who already has a
large results page
posted. Below are some results I have found. Some of these are also on
Karl's page, for solutions that I either found first, or found
independently before seeing them on his solutions page.
The object of this challenge is to tile rectangles and squares with
squares in a "nowhere-neat" way. Nowhere-neat means that no two squares
share two vertices and an entire edge.
A secondary challenge is to tile rectangles and squares without same-size squares sharing any segment of edge. These may be called "no-touch" solutions.
Tilings on this page: 11x15, 16x16, 19x19, 20x20, 20x85, 22x40, 23x23 (*), 27x27 (*), 28x43, 28x48, 32x32 (*, two solutions), 35x35 (*, two solutions), 37x37 (*), 38x38 (*), 39x39, (two solutions), 40x40 (two solutions, one *), 45x45, 47x47, 53x53 (two solutions), 55x55, 56x56, 59x59 (two solutions), 60x60, 65x65, 68x68, 71x71, 75x75, 83x83, 98x98, 105x105
(*) Different than the solution(s) on Karl's page for this size.
* marks no-touch solutions:

11x15 *

16x16 *
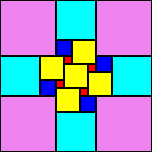
19x19
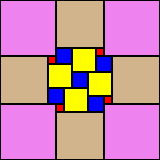
20x20

20x85 *

22x40

23x23

27x27 *

28x43

28x48
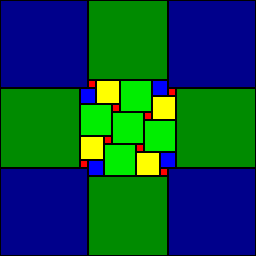
32x32

32x32 *

35x35

35x35

37x37

38x38

39x39 *
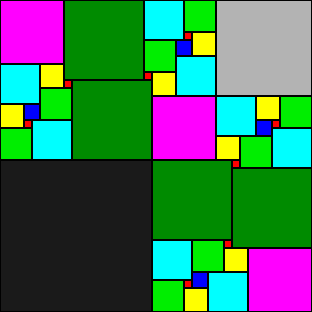
39x39

40x40
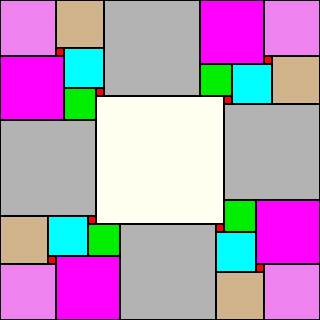
40x40 *
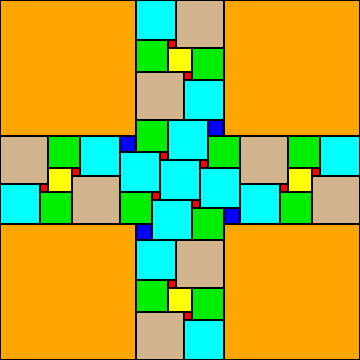
45x45

47x47 *

53x53

53x53 *

55x55 *
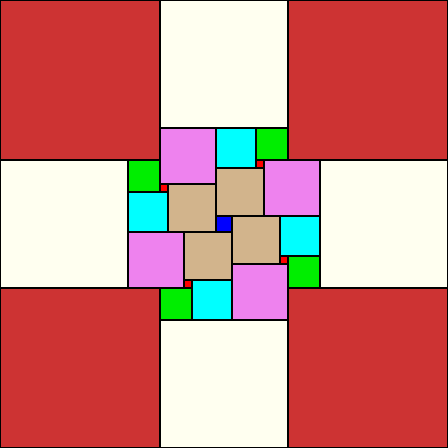
56x56

59x59 *

59x59

60x60

65x65

68x68 *
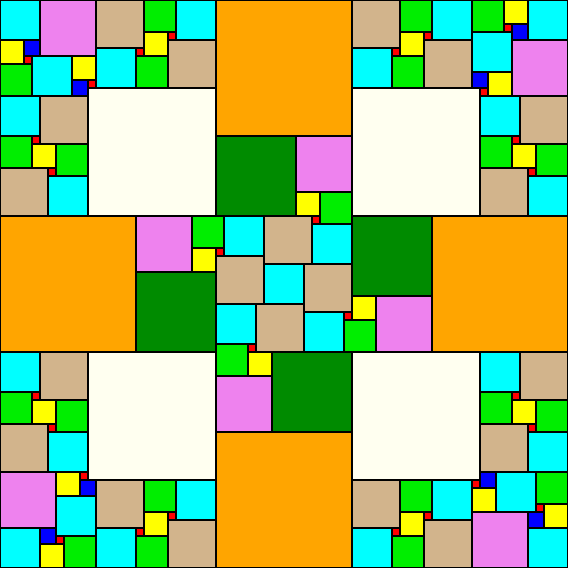
71x71
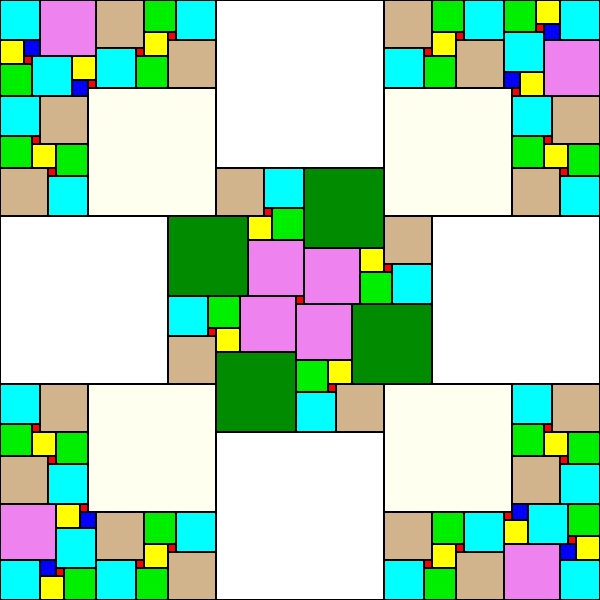
75x75

83x83

98x98

105x105 *
 11x15 *
11x15 * 16x16 *
16x16 *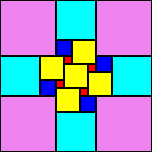 19x19
19x19 20x20
20x20 20x85 *
20x85 * 22x40
22x40 23x23
23x23 27x27 *
27x27 * 28x43
28x43 28x48
28x48 32x32
32x32 32x32 *
32x32 * 35x35
35x35 35x35
35x35 37x37
37x37 38x38
38x38 39x39 *
39x39 * 39x39
39x39 40x40
40x40 40x40 *
40x40 *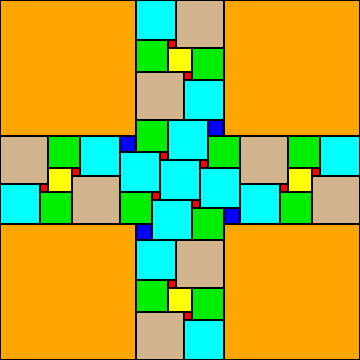 45x45
45x45 47x47 *
47x47 * 53x53
53x53 53x53 *
53x53 * 55x55 *
55x55 * 56x56
56x56 59x59 *
59x59 * 59x59
59x59 60x60
60x60 65x65
65x65 68x68 *
68x68 *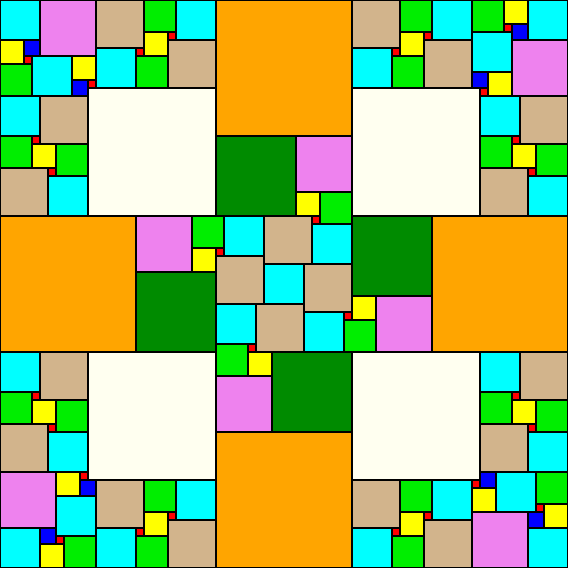 71x71
71x71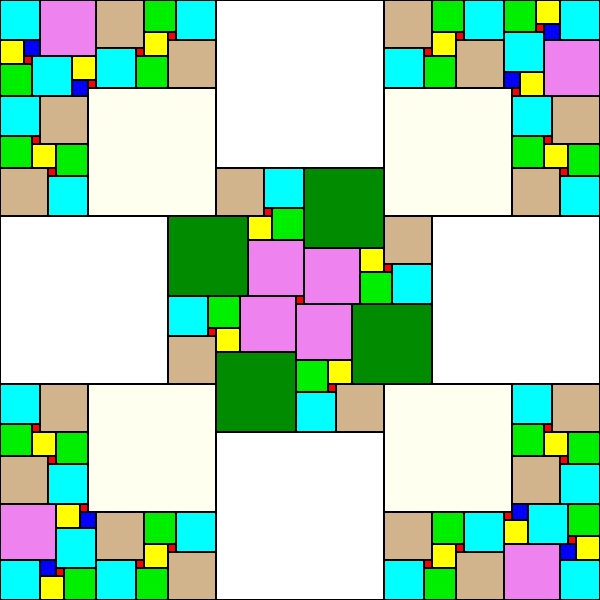 75x75
75x75 83x83
83x83 98x98
98x98 105x105 *
105x105 *